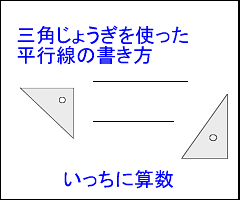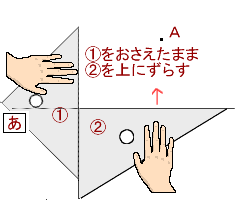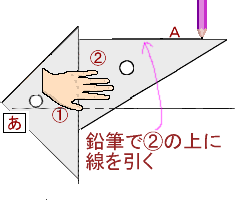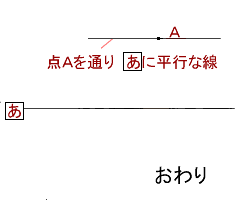
4年算数 垂直 平行と四角形 1 教え方のポイント
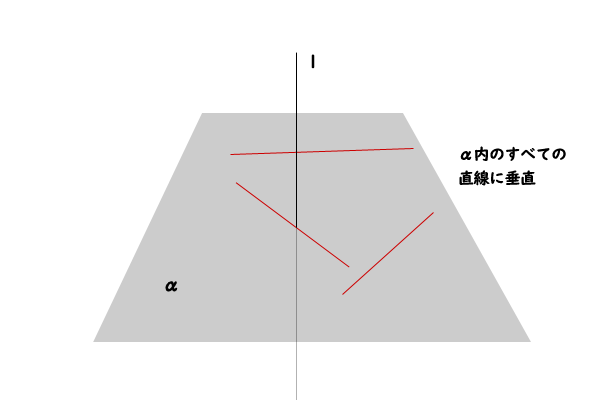
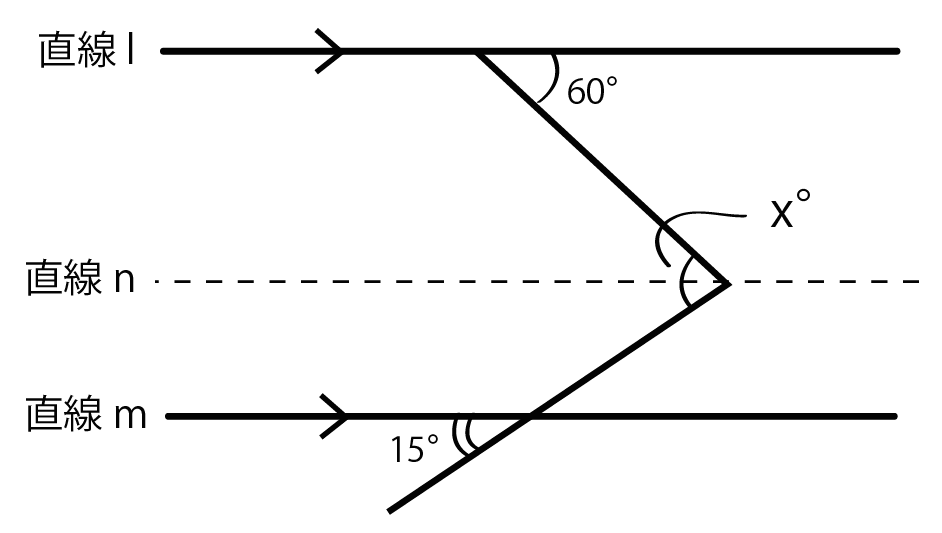
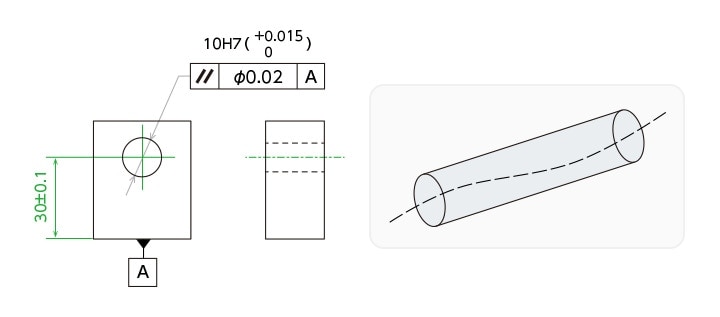
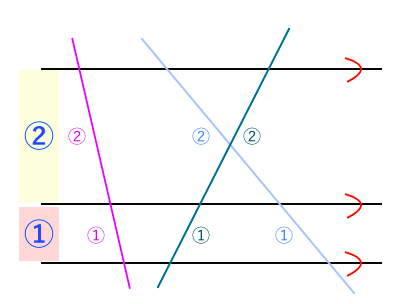
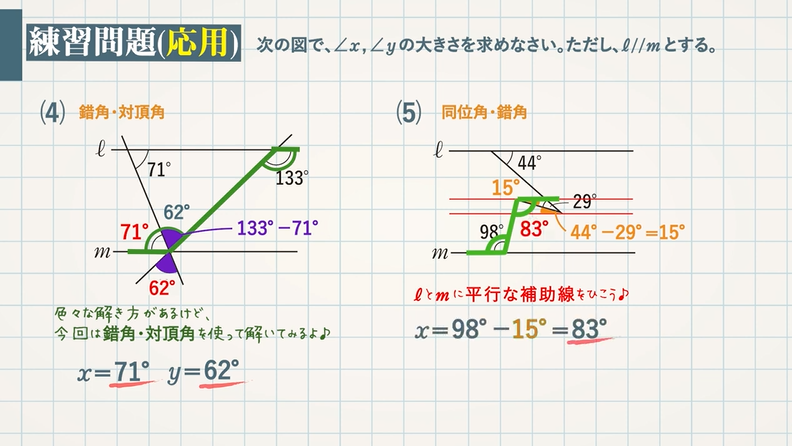
平行度 公差 記号 公差域の定義 指示方法及び説明 𝒕=003 𝒕=003 𝒕=001 公差域はデータムに平行な直径𝒕の円 筒によって規制される。 公差域は、距離𝒕 だけ離れ、データ ム平面bに平行な 平行2平面によっ て規制される。 公差域は、距離𝒕 だけ離れ、データ ム平面cに平行な 平行2平面にそれでは、平行線と角の特徴 (性質)を見ていきましょう 人は、「特徴」があると「名前」をつけたくなりますね! 口には出さなくても、心の中で「あの『茶髪君』いけてる! 」などなど、 名前をつけた、=『特徴がある』 ということですね! それでは、2本の平行線とそれを横切る直線について、3つほど。 前提として、『 直線は、180° 』ですね! あまりに
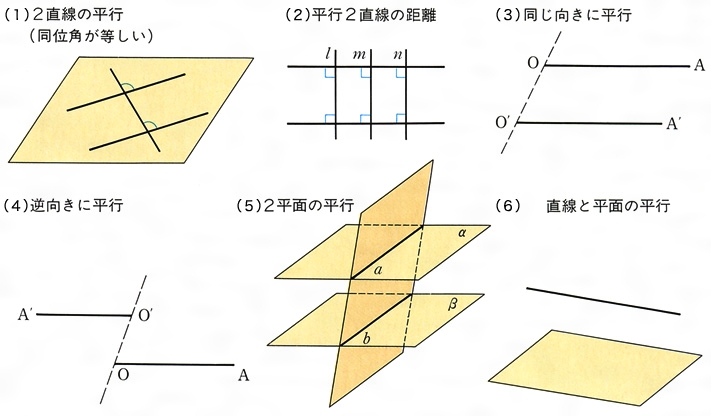
平行の定義
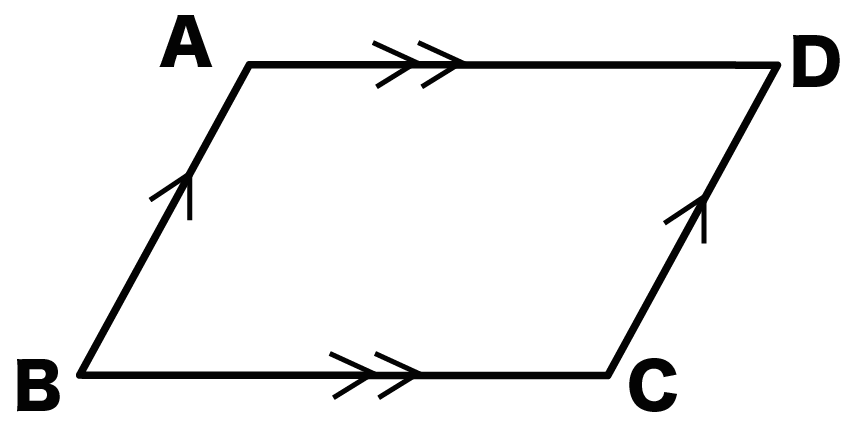
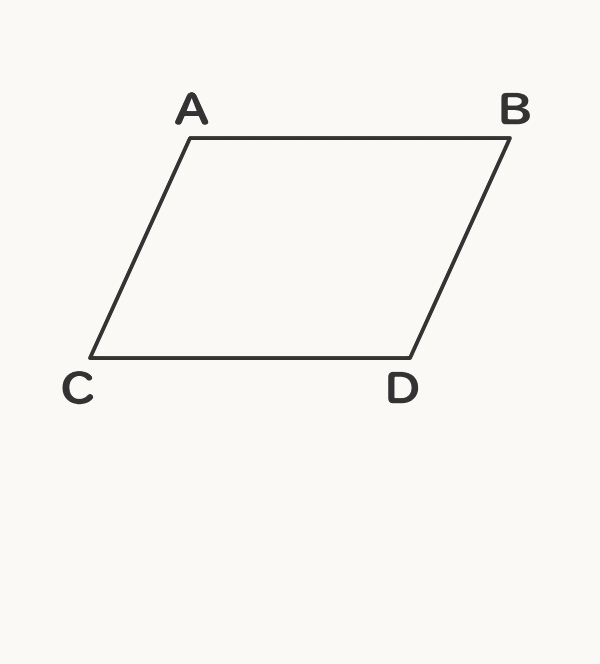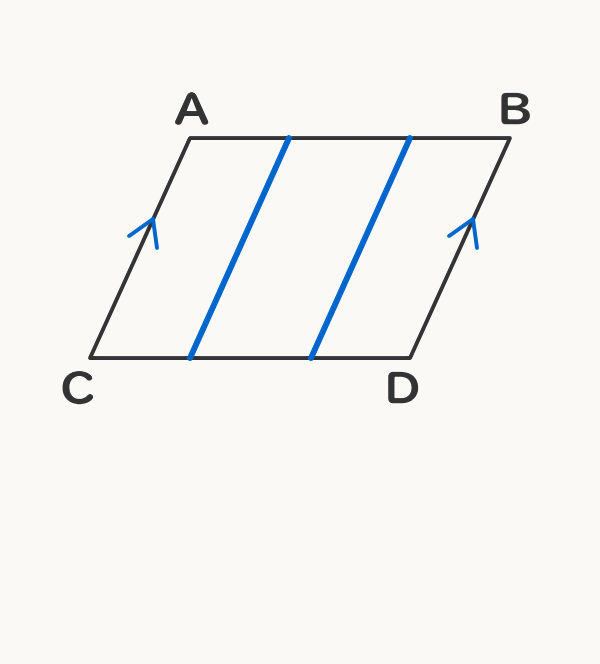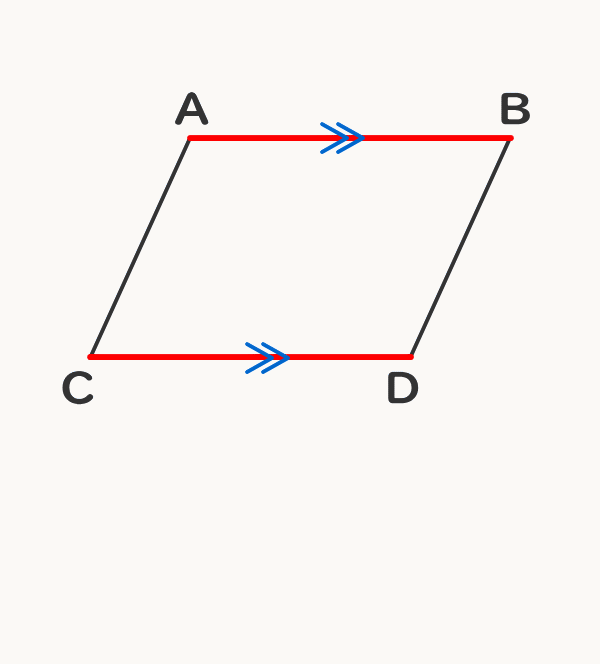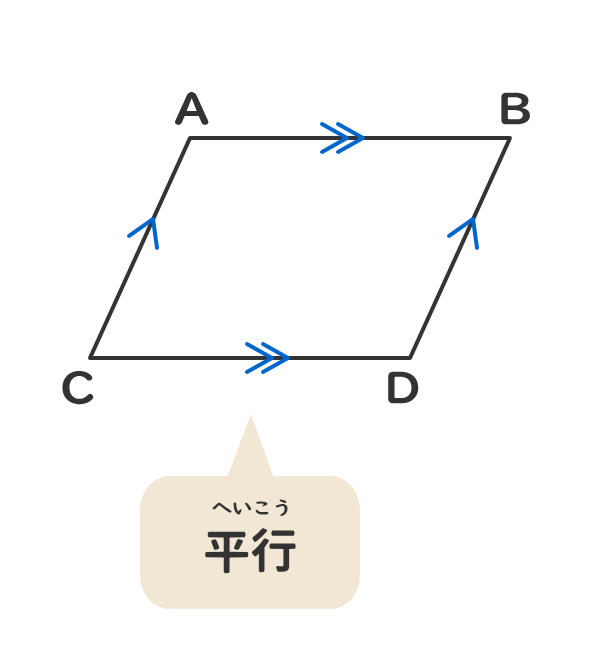
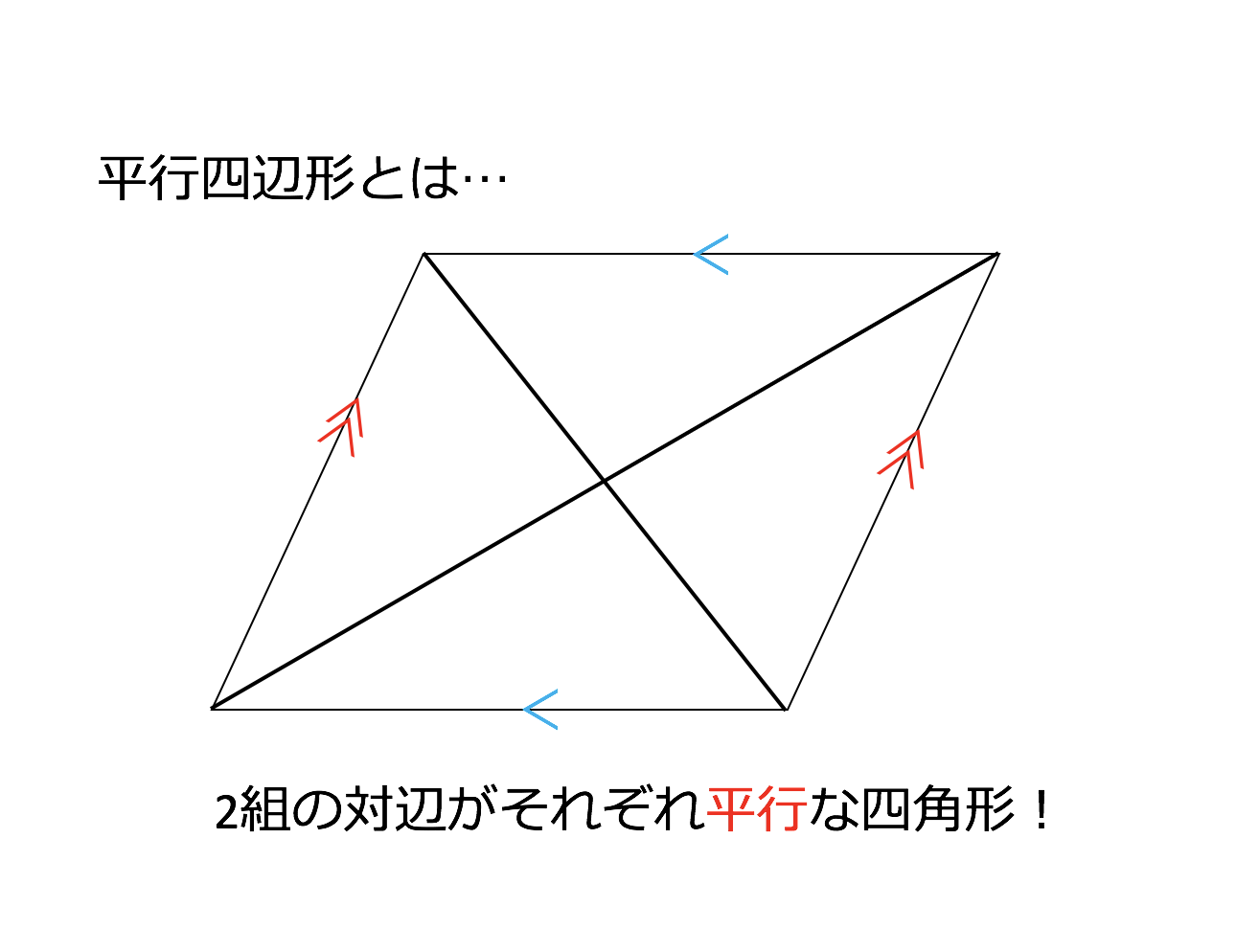
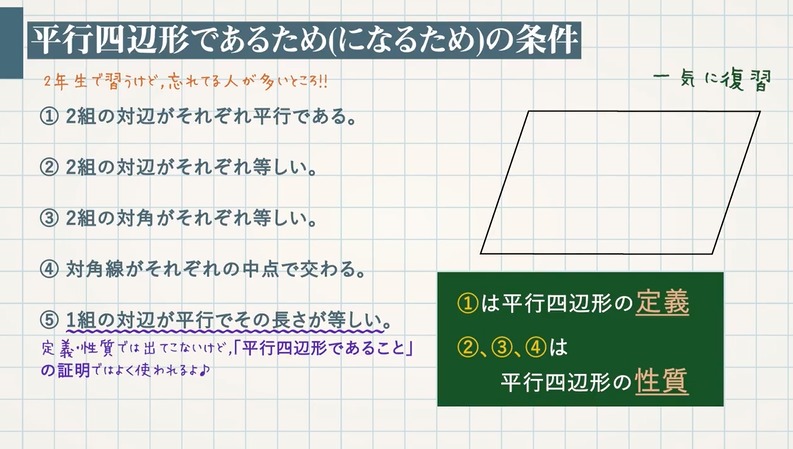
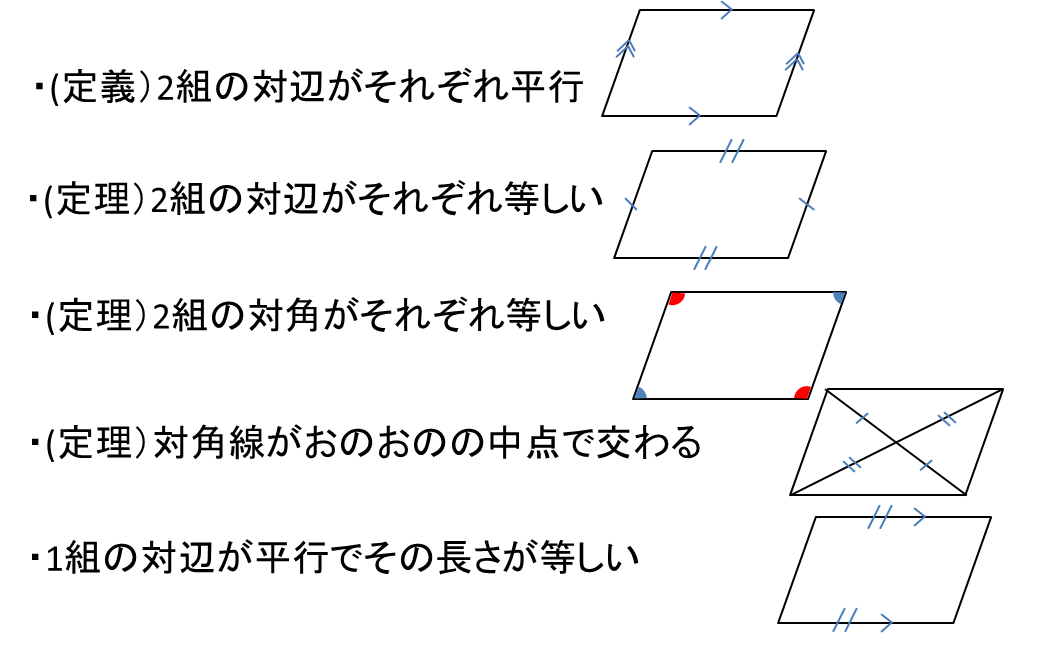
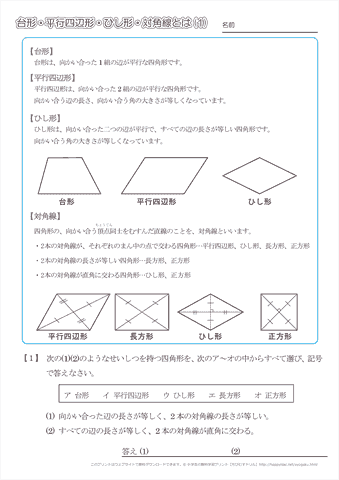
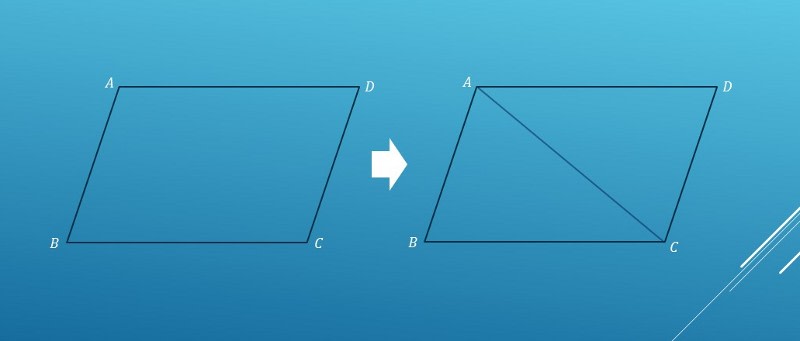
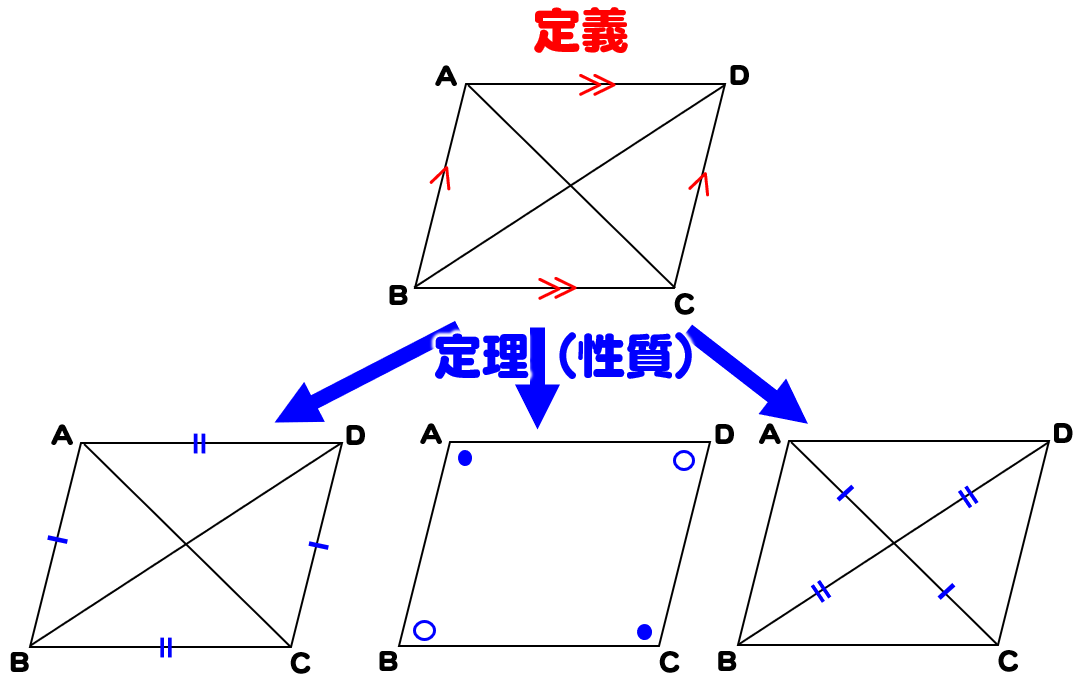
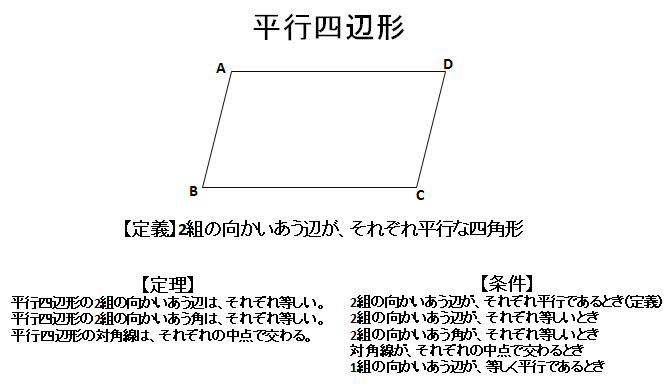
平行の定義-幾何偏差の定義及び表示 Definitions and Designations of Geometrical Deviations 1 適用範囲 この規格は,対象物の形状偏差,姿勢偏差,位置偏差及び振れ(以下,これらを総称して 幾何偏差という。)の定義及び表示について規定する。 備考 幾何偏差の許容値である幾何公差の記号による表示及びそ 平行四辺形とは、 \(\bf{2}\) 組の向かい合う辺がそれぞれ平行な四角形 のことです。 まずはこの定義をしっかり覚えておきましょう。 平行四辺形の性質(定理)
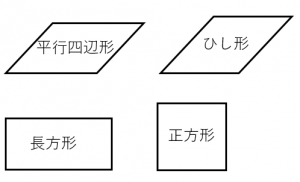
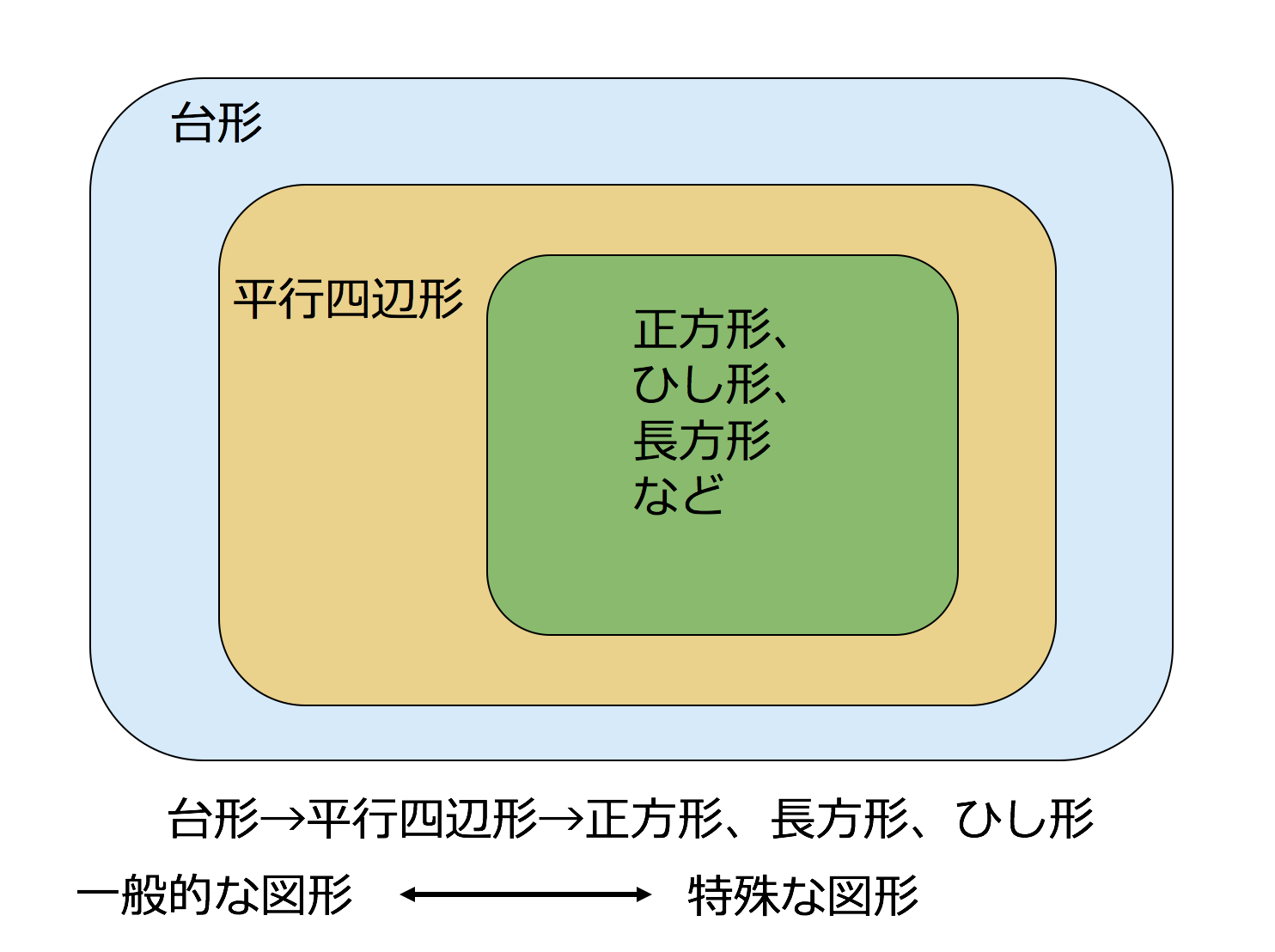
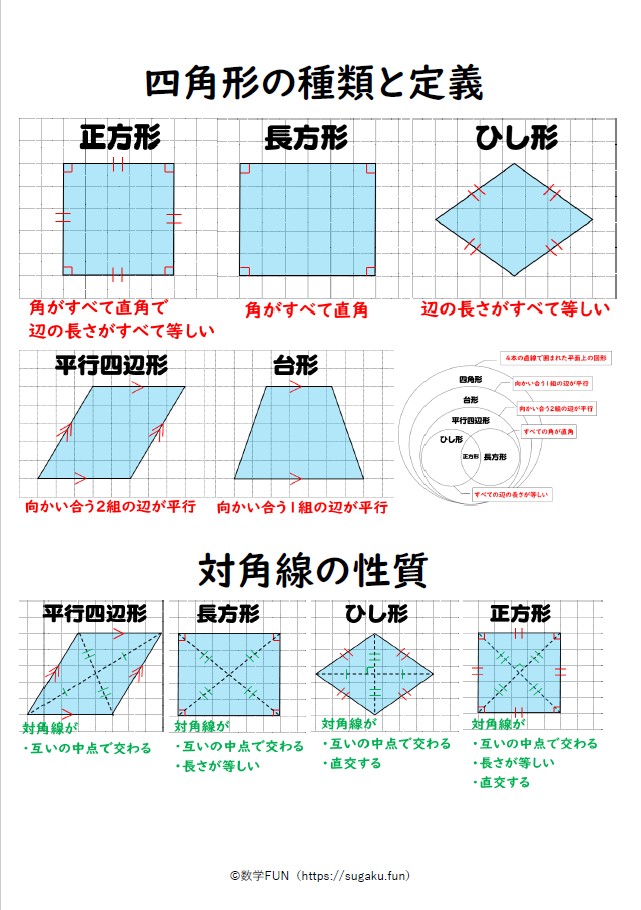
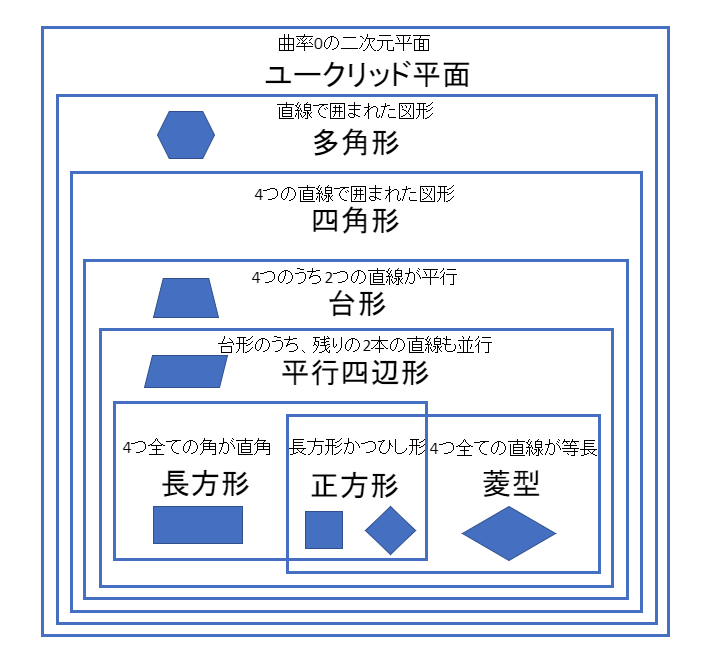
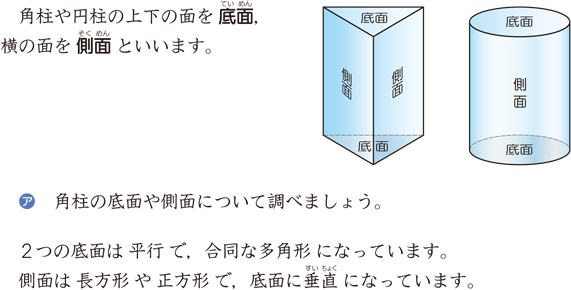
四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
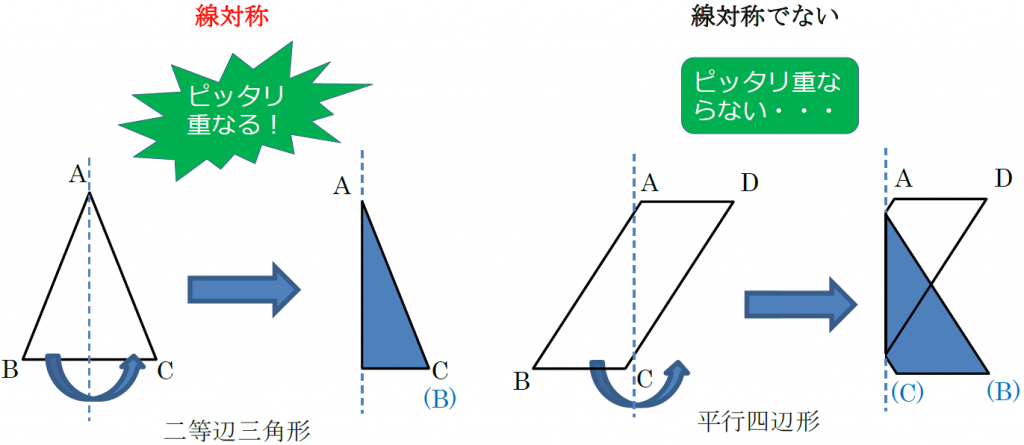
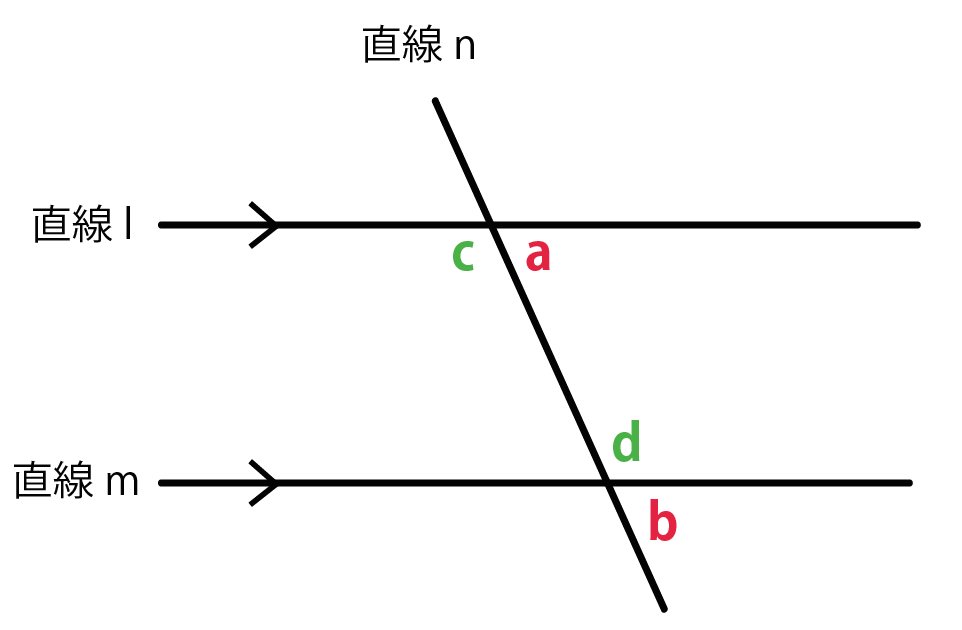
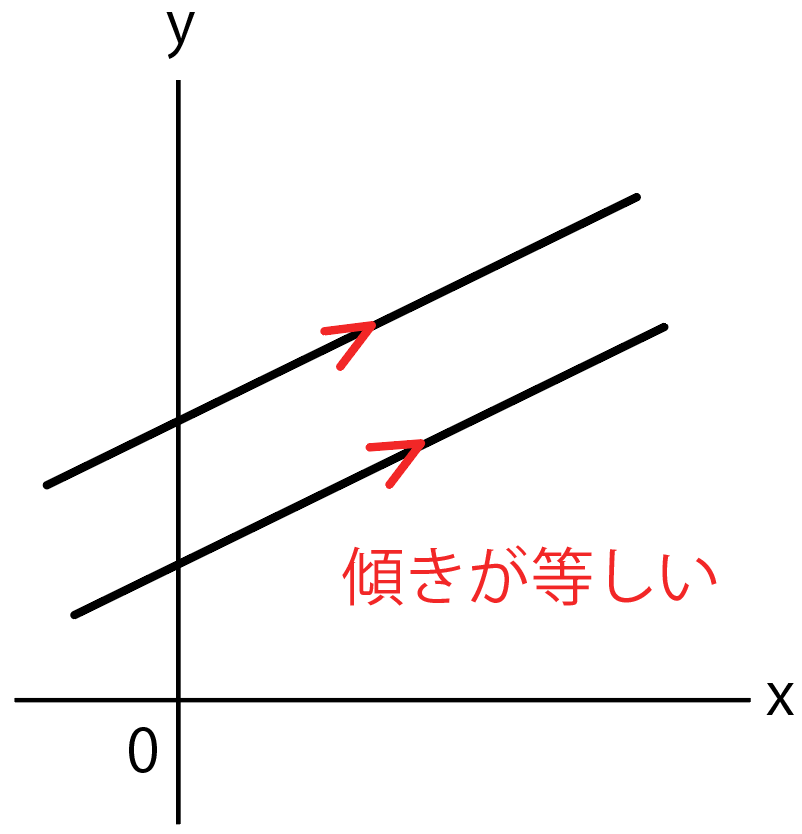
平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明できるでしょうか。 しっかり定義を押さえておきましょう。 平行四辺形2組の対辺がそれぞれ平行である四角形のこと。 図で表すとこうなります↓↓↓ ただ、ここからわかることはこれだけではありません! このように定義 定義 15 において平行線は以下のように導入される「同じ向きを持つが一つの同じ直線の部分となっていない直線を平行線と呼ぶ」 。 オーガスタス・ド・モルガン はこの教科書を批評して、主にこの定義およびウィルソンが平行線に関する内容を証明するのに用いた方法に基づいて誤りであ日本大百科全書(ニッポニカ) 平行の用語解説 同一の平面上にあって交わらない2直線を平行であるという。2直線が平行のとき、これに別の直線が交わってできる同位角は等しい(図(1))。逆に平面上で、2直線が別の直線と交わってできる同位角が等しければ、この2直線は平行である。また、平
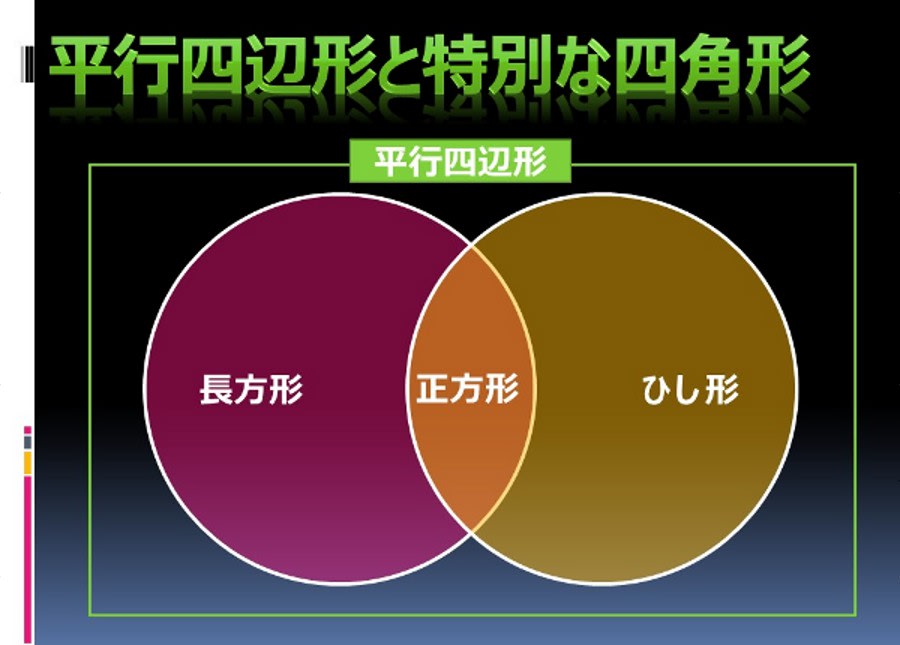
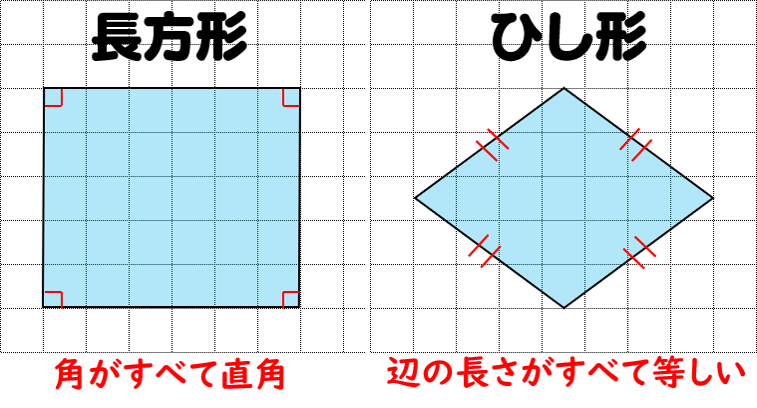
平面度は「1つの面」が測定対象であること、平行度は「2つの部品(部分)」が測定対象であることが、その違いです。 平面度と平行度は、測定する対象箇所と測定方法が異なります。 平面度(Flatness) 1つの面の平らな度合い(均一性)を示す数値。ひし形は平行四辺形の仲間??? 3分でわかる!ひし形(菱形)の定義 教科書によると「ひし形の定義」は、 4つの辺がすべて等しい四角形 だ。 ぜんぶの辺が等しい四角形。 ちょうどダイアモンドみたいなやつだね。 これが「ひし形」ってわけさ。 2平行度 jisでは、「データム直線、データム平面に対して平行な幾何学的直線または幾何学的平面からの平行であるべき直線形体又は平面形体の狂いの大きさ」と定義されています。 翻訳すると・・・
平行の定義のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「平行の定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
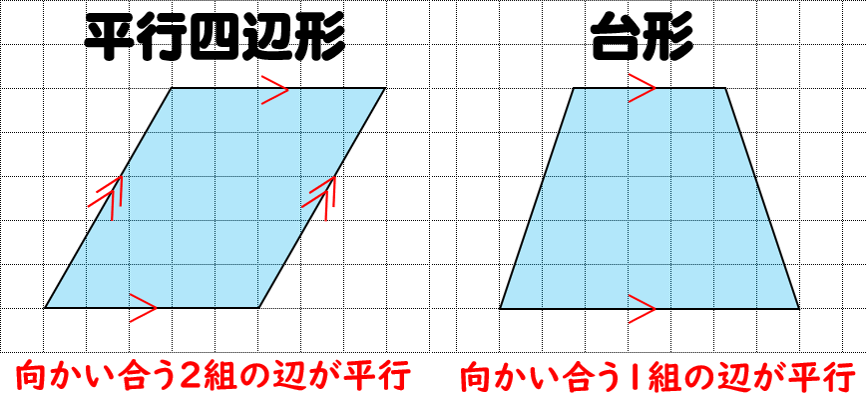
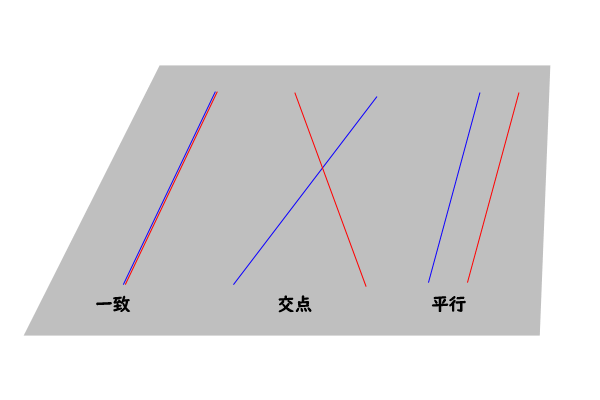
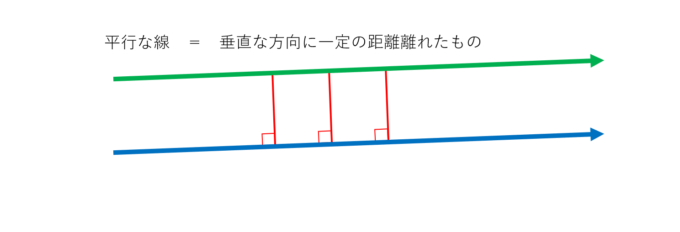
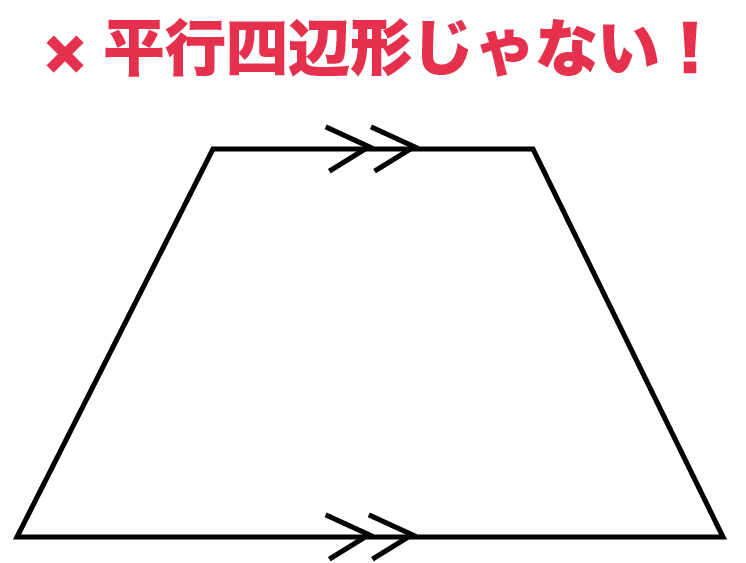
平面における直線の垂直・平行は,2本の直線の位置関係を表しています。 位置関係ですので,2 本の直線の長さには,全く関係ありません。 位置関係を成立させる条件だけを保っていれば,それで十分です。 その条件として示されてくるのが,垂直の場合であれば,「2つの直線が直角に交わる」ということです。 この条件を満たしさえすれば,2つの直線は常に平行四辺形: 向かい合う2組の辺が平行な四角形 台形: 向かい合う1組の辺が平行な四角形 注意点として、 "長方形" や "ひし形" も向かい合う辺は平行なので 『平行四辺形の定義』 に当てはまりますし、 "正方形" は 『長方形・ひし形の定義』 にも当てはまります。 つまり どんな"正方形"も"長方形"であり、"ひし形"でもあり、"平行四辺形"でも
Incoming Term: 平行の定義, 平行の定義 小学校4年,




0 件のコメント:
コメントを投稿